|
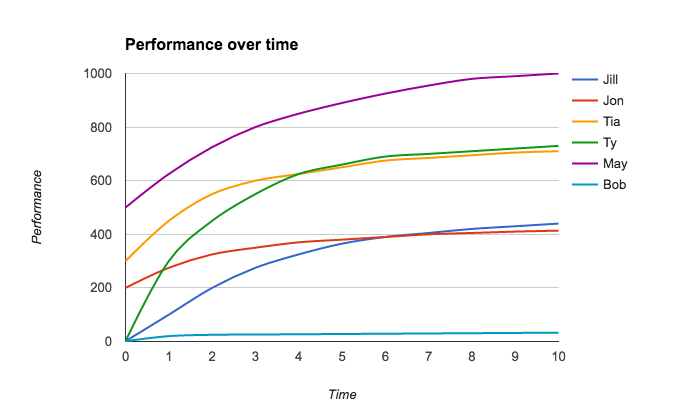
Above are six learning curves representing six hypothetical persons. You can see a variety of initial performance levels, going from 1 for Ty, Jill, and Bob at time 0, all the way up to 500 for May. You can also see a variety of ending performance levels, going from 33 at time 10 for Bob, all the way up to 1000 for May. All of the learning curves on the diagram above improve over time, as represented by increased performance over time and all have different rates of improvement over time. The question I want to answer is, “Can all students can learn?” It depends. In the above learning curves, all students show improvement. However, that means almost nothing given the different rates of improvement and absolute performance levels over different time periods. In fact, the idea that growth rates or proficiency levels (performance levels) tell us anything at all is patently absurd once the above curves sink in. Let’s start by measuring some growth rates. Bob (light blue curve) went from a performance level of 1 to a performance level of 33. Bob’s percentage change = (33-1/1) x 100 = 3200% We could also state that Bob is 33 times “better” at time 10 than he is at time 0. Either way, that’s a lot of improvement if we compare it to May (purple curve). May’s percentage change = (1000-500/500) x 100 = 100% We could also state that May is 2 times “better” than when she started. Clearly Bob has much more “growth” than May if we use simple percentage change formulas to find a growth rate. However, if we switch from growth rates to proficiency levels as measured by the absolute performance levels, we find that May is 30.3 times (1000/33) “better” than Bob. If we had a school initiative that made sure certain minimums were met, should it measure those minimums using growth rates or proficiency levels? If we set the minimums using growth rate targets at 500%, May (100%) is falling behind, but Bob (3200%) is doing great! He meets the minimum after time 1, whereas May never reaches the target. If we set minimums using proficiency levels and use a performance level of 400, then May (500) meets the target at time 0, while Bob (33) is still 377 points shy at time 10. If we look at the other people in the diagram above while using the same targets, either 500% growth or a 400 proficiency level, we run into similar problems. Tia never reaches the growth target, but does cross the 400 target by time 1. Ty crushes the growth target and also meets the proficiency target by time 2. Jon never reaches the growth target, but reaches the proficiency target after time 7. Jill meets the growth target easily, but takes until time 7 to reach the 400 proficiency target and we can easily imagine her curve never crossing the proficiency threshold by simply shifting it down a bit. The above presents serious problems for standards-based initiatives like the hypothetical one above. A number of students will be measured as falling behind depending on how we select our targets. Furthermore, even if we agree to the target, there is the pesky question of time allowed to meet it. If the target is set at a 400 proficiency level, but it is expected to be met by time 1, only Tia and May will reach it. If we allow until time 6, we can add Ty. If we extend it to time 7, we include Jill and Jon. Many schools, districts, and nations use metrics similar to the above for measuring student learning. The United States has No Child Left Behind, but is by no means the only one to measure student learning with some type of standards. It began under a proficiency model of measuring absolute performance, but has since begun shifting to growth models in several states. The OECD has PISA. The International Baccalaureate uses proficiency levels with its standards-based rubrics. It should be clear that both growth and proficiency metrics have inherent problems. The above is aimed at showing how absurd many student measurements of learning can be. Success and failure are totally dependent on the metrics we decide to use. That only becomes worse the more variables we measure. For example, let’s assume the above learning curves are for math. What happens when we add language and find students with language learning curves that don’t match their math learning curves. Perhaps, Bob and May are completely reversed and we find May with low absolute performance levels and Bob with high absolute performance levels. Do they both count as failing if we require a proficiency level of 400 for both math and language? I recently finished Why School?, by Will Richardson, who stated the following in his book’s final pages, I can’t wait 10 to 20 years. By that time, our kids will have long since graduated, and the story of what schools become will have already been written. I hope they are places where adults and children come together to learn about the world, places rich with technology that lets our kids dream big and create things to fuel those dreams. I hope schools will be places where learning is fun, where it’s not so much about competing against one another as about working together to solve the really big problems we’ll face together in the years ahead. (Kindle Locations 559-562) That seems right to me.
Let’s return to the initial question, “Can all students learn?” Of course, but what that means is up for debate. If it means hitting a particular standardized level of proficiency or growth, then no. Some students will never reach particular growth or performance levels selected for them. However, if, as Richardson writes elsewhere in his book, it means that students, "have the skills and dispositions they need to solve whatever hard problems come their way, and [that] they’ll know how to go about creating something of value and sharing it with the world,” then YES! (Kindle Locations 543-544).
0 Comments
Leave a Reply. |
Archives
November 2017
|
 RSS Feed
RSS Feed